Was ist Modellbildung und Simulation?

Modellbildung und Simulation beschreibt neben Theorie und Experimenten eine Methodik, Probleme zu lösen. Der Begriff „Modell“ wird in vielen Anwendungsgebieten verwendet und bezeichnet dabei oft sehr unterschiedliche Angelegenheiten. Es gibt unter anderem Datenmodelle, Architekturmodelle oder statistische Modelle. In diesem Artikel ist bei einem Modell immer die Rede von einem Simulationsmodell.

Als Simulationsmodell wird ein Abbild eines realen Systems bezeichnet, mit dem erstens die inneren Vorgänge in diesem System untersucht werden können und zweitens Tests in diesem System durchgeführt werden können. Der Nutzen ist, dass dadurch Erkenntnisse gewonnen werden, die eine Fragestellung beantworten und dadurch helfen, ein Problem zu lösen. Simulationsmodelle kommen häufig dann zur Anwendung, wo „Was wäre wenn“-Fragen gestellt werden, die mit Statistik nicht mehr zu beantworten sind, weil die Eigendynamik des Systems eine Rolle spielt.

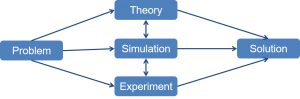
Modellbildung und Simulation wird auch als dritte Säule neben Theorie und Experiment zur Lösung von Problemen bezeichnet.

Aber wie funktioniert das konkret? Es gibt unterschiedliche Methoden, ein Simulationsmodell zu bauen. Die Bearbeitung eines Modellierungsproblems sollte immer einem Modellierungsprozess entsprechen, welcher die notwendigen Arbeiten in eine klare Struktur bringt. Dieser Modellierungsprozess ist unabhängig davon, mit welcher Methode das Simulationsmodell gebaut wird.

Der Modellierungsprozess

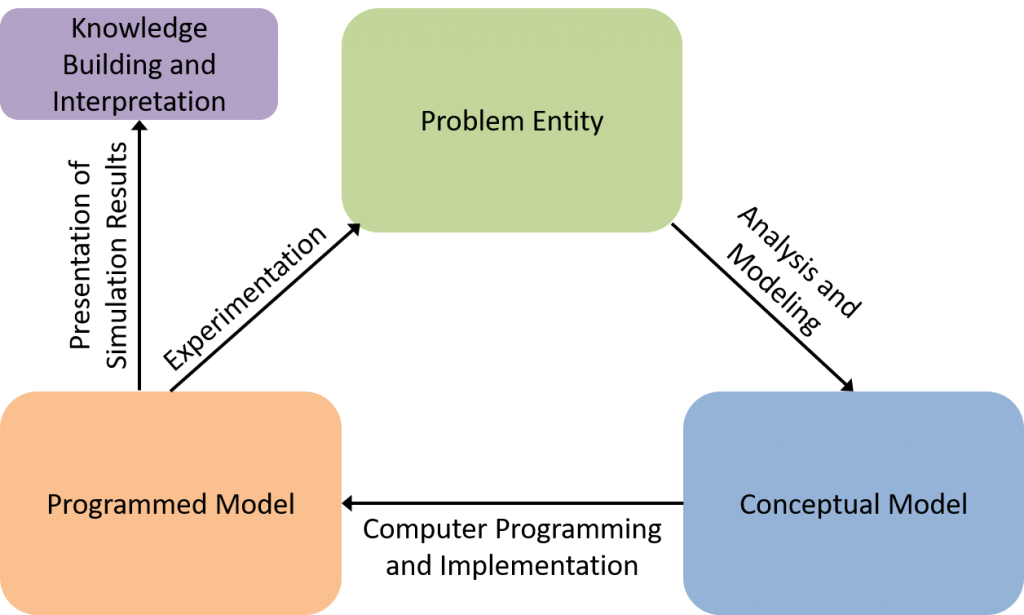
Der Modellierungsprozess besteht aus vier verschiedenen Teilen.

Eine Übersicht über den Modellierungsprozess

Problem Entitiy

Ein Modellierungsproblem beginnt immer damit, das zugrundeliegende Problem zu betrachten und Fragen zu formulieren, die mit dem Modell beantwortet werden sollen. Danach wird das reale System analysiert. Dies umfasst nicht nur eine quantitative Beschreibung, sondern auch eine qualitative Beschreibung der Strukturen und Zusammenhänge. Dazu sind häufig Datenanalysen notwendig, aber auch Informationen aus der Literatur und fachliches Expertenwissen.

Conceptual Model

Zunächst wird durch eine Evaluierung der Eigenheiten sowie der Vor- und Nachteile festgelegt, mit welcher Methode das Modell umgesetzt wird. Danach ist ein Konzept zu verfassen, wie das reale System bestmöglich als Simulationsmodell umgesetzt werden kann. Das Modell ist immer eine vereinfachte Darstellung des realen Systems. Dabei ist zu prüfen, welche Vereinfachungen akzeptabel sind, und welche Strukturen möglichst detailgetreu umgesetzt werden müssen.

Programmed Model

Im nächsten Schritt wird das Konzept implementiert. Falls verfügbar, kann dazu auf eine Entwicklungsumgebung oder ein Framework zurückgegriffen werden, oder es wird komplett selbst in einer geeigneten Programmiersprache implementiert.

Danach wird das Modell simuliert und es werden Tests durchgeführt. Häufig stößt man dabei auf Probleme, Fehler oder Unzulänglichkeiten. Dann durchläuft man den Modellierungsprozess erneut, führt weitere Analysen in der Problem Entity durch, adaptiert das Konzept und setzt es im Programmed Model um. Dieser Kreislauf wird so oft durchlaufen wie nötig.

Knowledge Building and Interpretation

Wenn das Simulationsmodell zufriedenstellend ist, werden die Resultate in eine verständliche Form zu gebracht, oft mittels Tabellen und Grafiken. Das ist in der Regel durch Interpretationen und Erklärungen zu ergänzen, um die Fragestellungen in einer allgemein verständlichen Form zu beantworten.

Modellierungsmethoden

Zur Erstellung eines Modells gibt es unterschiedliche Methoden.

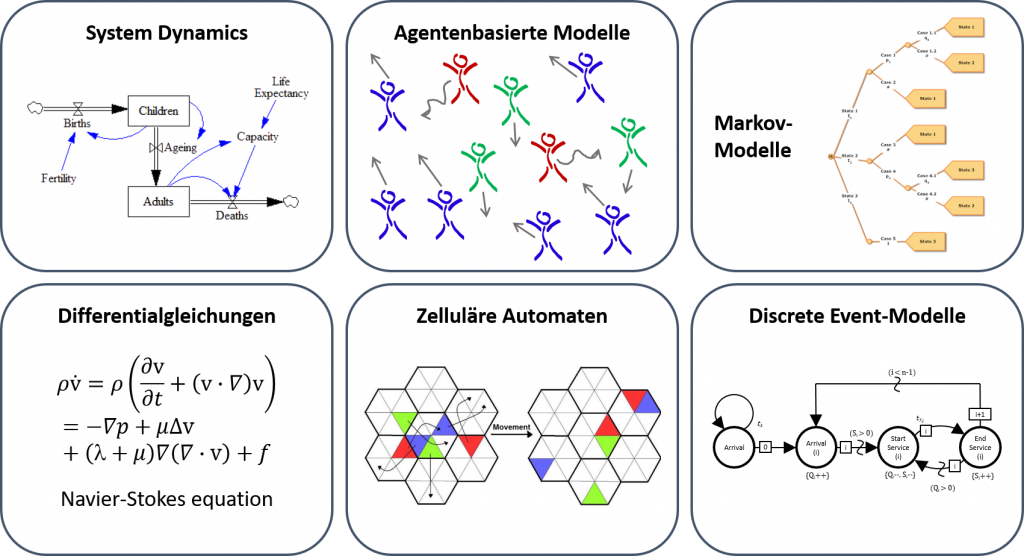
Schematische Darstellung wichtiger Modellierungsmethoden: System Dynamics, Agentenbasierte Modelle, Markov Modelle, Differentialgleichungen, Zelluläre Automaten, Discrete Event Simulation

Differentialgleichungen

Differentialgleichungen sind die älteste Form von Simulationsmodellen, die bereits lange vor der Erfindung des Computers existierten. Beispielsweise konnte man damit schon vor Jahrhunderten physikalische Problemstellungen wie Flugbahnen von Objekten berechnen. Heutzutage finden Differentialgleichungen bei einer Vielzahl von physikalischen Problemen Anwendung. Die Berechnung findet in der Regel mit hocheffizienten Computerprogrammen in Form von numerischen Differentialgleichungslösern oder Finite Elemente Methode statt.

System Dynamics

System Dynamics ist eine graphische Darstellung von Flussdiagrammen. Diese werden im Hintergrund mittels Differentialgleichungen realisiert, ohne dass der Anwender diese kennen oder verstehen muss. System Dynamics wurde in den 1950er Jahren durch Jay W. Forrester am MIT entwickelt. Die Methode erlangte durch den Club of Rome Berühmtheit, der mit dem „World3“-Modell die weltweite Entwicklung von Bevölkerung, Nahrung, Industrie und dem Ökosystem darstellte. Heute stehen ausgereifte Frameworks wie Anylogic oder Vensim zur Verfügung.

Discrete Event Simulation

Discrete Event Simulation kommt ursprünglich aus der Logistik, wo einzelne Objekte dargestellt werden, die in verschiedenen Stationen bearbeitet werden und dabei unterschiedliche Zustände annehmen können. Heute wird diese Methode auch in anderen Bereichen angewendet, beispielsweise in der Medizin, wo die Krankheitszustände von Patienten simuliert werden können. Zur Implementierung existieren einige Simulatoren wie beispielsweise Arena.

Markov-Modelle

Markov-Modelle dienen dazu, ein System zu simulieren, das verschiedene Zustände annehmen kann. Anwendungen in der Gesundheitsökonomie beispielsweise bauen auf Entscheidungsbäumen auf und zeigen die Auswirkungen von unterschiedlichen strategischen Entscheidungen. Als Simulator steht beispielsweise TreeAge zur Verfügung.

Zelluläre Automaten

Diese Methode beschreibt Zellen, die auf einem Raster angeordnet sind. Eine erste, bekannte Umsetzung ist John Conway’s Game of Life, in der mit schwarzen und weißen Zellen bestimmte Muster erzeugt werden. Derartige Techniken wurden Anfang der 2000er-Jahre von Stephen Wolfram weiterentwickelt. Die häufigsten Anwendungen finden sich heutzutage in der Simulation von fließenden Flüssigkeiten (beispielsweise Wasser in Rohren oder Blut in Blutgefäßen).

Agentenbasierte Modellierung

Dabei werden die Objekte eines Systems mit individuellen Verhaltensweisen umgesetzt, die dann selbstständig miteinander interagieren können. Dadurch ist es möglich, Systemverhalten in einer Komplexität abzubilden, die mit anderen Methoden nicht darstellbar ist. Allerdings sind dazu große Rechenleistungen notwendig, welche erst seit wenigen Jahren zur Verfügung stehen. Aufgrund des enormen Potentials erfährt die agentenbasierte Modellierung seit Mitte der 2000-er Jahre einen weltweiten Boom, der nach wie vor anhält. Die Anwendungen decken die unterschiedlichsten Bereiche ab und umfassen Fluchtwegsimulationen in Gebäuden ebenso wie Wirtschaftssimulationen oder die Ausbreitung von Epidemien. Mittlerweile steht eine Fülle an Simulatoren wie Anylogic oder Frameworks wie Mason oder Repast zur Verfügung.

Fazit

Modellbildung und Simulation setzen dort an, wo Wissen über Systeme benötigt wird, das mit herkömmlichen Berechnungen nicht gewonnen werden kann. Die Kunst besteht darin, für konkrete Fragestellungen die bestmögliche Methode auszuwählen, das reale System geeignet zu abstrahieren und korrekt als Modell umzusetzen. Da ein Modell immer eine Vereinfachung darstellt, ist es unerlässlich, die Bereiche einzuschätzen, in denen ein Modell gültig ist und Ergebnisse in zufriedenstellender Qualität liefert.

Es handelt sich dabei um ein stark interdisziplinäres Gebiet, da sowohl die Modellierungsmethodik beherrscht, als auch das jeweilige reale System verstanden werden muss. Die Anwendungen erstrecken sich über die unterschiedlichsten Disziplinen und erfordern dort häufig spezialisierte Modellierungsexperten. Die Zukunft der Modellbildung und Simulation besteht sicherlich darin, die Methoden für bestimmte Anwendungen weiterzuentwickeln und miteinander zu kombinieren.